注意 ＜当ニュースを閲覧する前に必ず以下の内容をお読みください＞
当サイトでは以下の規則が存在し、この趣旨に違反した場合、一人当たり200万円以下損害賠償請求をする場合がございます
１．当サイトの全ての情報の著作権は、サイト開設者である山下信義に属する
２．当サイトに書かれているいかなる内容も金銭目的、または金銭収入につながるような使用を禁ずる
３．無料で他者に提示するときは、必ず当サイトのURLや存在を知らせる
４．また無料で教えた者にも、必ず当サイトの規則のことを伝えること
５．仮に伝えなかった場合、伝えられなかった者が、規則を守らず起こした損害は、伝えなかった者が損害賠償請求の対象になるとする
６．仮に改変や改良をした場合であっても、必ず当サイト開設者である山下信義に連絡を取り、改変、改良をどのようにしたか内容を知らせること
７．なお、改変や改良された内容が有効である可能性が高い場合、当サイトでも公開してもいいとする
８．１以外の上記の規則は当サイト開設者である山下信義本人には適用されないものとする
このニュースではトップページにある対文章式記憶術の解説をしていくことにします。
トップページにある対文章式記憶術の解説は、理論的な背景などをすっ飛ばして説明しているし、やり方なども飛ばしているため、非常にわかりにくかったと思い、このニュースを出すことにしました。
まずこの前に書いたニュースの
トップページ
で、一般的記憶術の知識を付けるために読んでおいてください。
では、対文章式記憶術の解説に入ります。
これは前のニュースの繰り返しになりますが、一般的記憶術のできることはほぼ単語の記憶や記号の記憶に限られます。
記号には数字なども含まれますが、基本的に単語の暗記です。
それでは、文章の記憶に関してはどうでしょうか？
文章の記憶に関してはできるのは、意味単位でイメージ化をして覚えることができます。
なぜ意味単位なのかというと、単語単位だと以下の問題が起きるからです。
それはインプットでは
①イメージの数が多すぎて、収拾がつかなくなる。
これは仮にジャーニー法や記憶の宮殿を使っても、場所が足りなくなるため問題の解決は難しいです。
②同じ単語が頻出するため、同じイメージができてしまい、干渉や検索の失敗が起きやすくなる
ここからはアウトプットです。
③抽象的単語をイメージ化した場合に、そのイメージから単語を思い出した際に、イメージが多義的に解釈されるために何を思い出せればいいのかわからなくなる
④イメージのため、どのイメージが始めなのかわからなくなり、順序が思い出せなくなる
と言ったことが起きるため、一般的記憶術では文章を単語単位で覚えることが難しくなります。
なお、順序に関しては場所法をする際の置き方に、規則を付ければ解決する問題ではあります。
上述の問題をほぼ解決したのが、対文章式記憶術です。
対文章式記憶術のコンセプトは脱場所法であり、想起スピードの高速化です。
この２点を理想として探究したのが、対文章式記憶術です。
対文章式記憶術ではまずインプットの問題点を解決しました。
最初の問題である上述①の情報量が多すぎるということはこのように解決しました。
ここで突然ですが、みなさん絶対的記憶力を自分は持っている！と断言できる方はおられるでしょうか？
絶対的記憶力とは、一回見るだけで記憶できる能力のことです。
ボブは自分には絶対的記憶力がある！と断言できます。
そしてそれはみなさんもほぼ同様でしょう。
そんなことを言うと、「そんなの持っているわけないだろう！」とツッコミを入れる方が大多数だと思われます。
でも考えてみてください。
日常を送る上で、一回で記憶できないとできないことはたくさんあると思いませんか？
例えば電車に乗るとき、改札でカードでお金を払ったかどうかということを、別にみなさん一々覚えている感覚すらないでしょ？
そんなことじゃなくても、例えば「この一個のリンゴという単語を覚えてくれ！」と言われたら、ほぼ全く忘れることなく覚えているのではないでしょうか？
これが絶対的記憶力です。
「そんなの量覚えてないからだ！」とツッコミを返す方がたくさんいるでしょう。
ですが、これも絶対的記憶力、つまり一回見たら忘れないはずですよね？
さて、こんな議論をする必要がどこにあると思われる方が大多数だと思います。
それは簡単です。
一個の情報を覚えていることによって、それを見るだけで何万個の情報にアクセスできる状態にすれば、絶対的記憶力に近い記憶が手に入るのです。
はてさて、そんな状況どこにあると思われるかもしれません。
ところが、あります。
それは連想です。
連想しまくれば、理論上一つの情報から、万に近い情報が展開できます。
さらに言えば、連想を制せれば、記憶しなくてもいい状態を作り出せます。
「そんな馬鹿な？！」と言われる方もおられるでしょう。
例えば「連想」という単語から、最初に思いつく単語が「そんな」で、次に思いつく単語が「馬鹿な」だったら、「そんな馬鹿な？！」は、「連想」という単語を覚えているだけで、覚えなくてもいいと思いませんか？
実際に出てくる単語は、もっとランダムであり、一つの単語の連想だけで、全てが説明つくということは、ほぼありません。
とはいうものの、理論上はランダムに出てきた単語を連想で引き出せれば、記憶はほぼしなくてもいいのです。
また、文章を覚える上でも、このような状態を作り出すのは必須です。
なぜならば、一般的記憶術では文章を大量に覚えると、イメージの数が多すぎて収拾がつかなくなるからです。
「え！？そんなのジャーニー法とか、記憶の宮殿で何とかできるじゃん！？」と思われる方もいらっしゃるでしょう。
しかしこのような場所法の延長では、文章を大量に覚えたとき、必ず場所が足りなくなります。
そこで情報をなるべく一つに、あるいは少なくする技術が必要になるのです。
では、この状態を目指せばいいということはわかってくれたと思います。
けれども、こんな状態、記憶術でどう再現すればいいんだ？ということになります。
一般的記憶術のおさらいで、「り」「ん」「ご」という三つの情報を一つのイメージである「リンゴ」に直していました。
このとき、重要なのが「情報の減少」という原理です。
三つの情報が一つの情報に書き直されている、ということが大事なのです。
実際に実験してみるとわかると思いますが、記憶術の情報の増加の側面だけみて、記憶するためには情報の増加をさせれば覚えれると考えると上手くいきません。
情報の増加とは先ほどの三つの文字情報に一つのイメージ情報が加わっているとも観て取れますね？
この情報の増加のみで、例えば「り」「ん」「ご」という文字を覚えたいから、「リンゴ」に加えてニュートンのイメージも付加しようと考えると上手くいきません。
何が上手くいかないか？というと、単純に文章だったら、全体の文章の“量”が覚えれなくなります。
「あれ？普通の記憶術で本の文章を10行覚えれたのに、情報の増加させた記憶術では５行ぐらいしか頭に残っていないなー？」です。
このように情報を付加させ、情報量を増加させた上で、情報の減少を起こすことが大事になるのです。
それでは、一個の情報に基づく絶対的記憶力を目指しつつ、連想でランダムに出てくる様々な単語を説明し、かつ情報の増加と減少を起こすにはどうしたらいいのでしょうか？
ここで出てくるキーワードが“まとまりの良さ”です。
まとまりの良さは一言で言うと、人のイメージに付随する「服」のことです。
なぜ「服」がまとまりが良いという言葉で表されるかというと、例えば服を着ていない人間もイメージすることができますが、「ほら、誰々さんを思い出してよ？」と言われたとき、ほとんどの人が「服」を着た誰々さんをイメージしますよね？
これって思い出すときに裸の誰々さんを思い出してから、イメージの中で「服」を誰々さんに着せているイメージなんてしていますか？
つまり誰々さんと服を思い出すときに時差がありますか？
ないですよねー。
ほとんどの人が誰々さんを思い出すときと服を同時に思い出しているはずですよね？
では、これが誰々さんの手だったり、誰々さんの足だったりした場合はどうでしょうか？
つまり誰々さんのパーツは誰々さんを思い出すときに時差がありますか？
これまたないですよね？
つまりです。
誰々さんと“まとまりが良い”イメージというのは、時差なしで同時に想起できるんです！
これを応用したのが、対文章式記憶術のパーツです。
ちなみに“まとまりが良い”という言葉は極めて漠然とした言葉です。
これの言い換えは、「既知の記憶で参照できるまとまった情報」が“まとまりが良い”という現象を起こす鍵です。
そこで、この鍵を使いましょう、となりますね？
ある任意の文章をパーツに直しただけでは、複数のパーツが同時に想起されることはありません。
先ほどの“まとまりが良い”という言葉の言い換えをよく考えてください。
既知の記憶、つまりすでに記憶していることで参照できる、つまり思い出せるまとまった情報という言い換えでした。
ようするに、すでに記憶している情報を多く含んだ情報のとき、同時に想起される、ということです。
ここで、疑問に思ってほしいのは、情報を多く含んだ情報という部分です。
ここで反対のことを考えてください。
情報を多く含まない情報って何？と。
丸い卓球の玉でさえも、情報を多く含んでいるとは思いませんか？
リンゴでさえ複雑なもので、情報を多く含んでいます。
唯一、記号の◯などは情報をあまり含んでいないように観えます。
そこで考えられるのは、記号でもない限り、巷に溢れている情報の多くは、情報を多く含んでいると考えられます。
ということは、パーツを何か別の情報に置き換えれば、同時に想起されるんじゃないか？ということに気づきます。
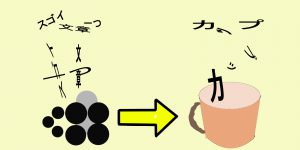
そこでパーツを何か別のイメージに置き換える、見立てることをすることで記憶に定着させようと画策したわけです。
例えば
トップページにある●はまさにそのパーツです。
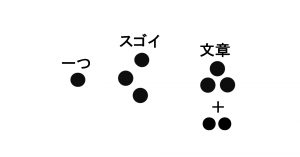
例えば
●
●●
●●
＋
●●
●
●
というパーツがあったら、組み合わせて、
●●●
●●●
●●●
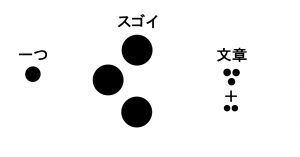
というパーツにすることができます。
これを今度は“正方形”に見立てることで、一つの情報にします。
これがパーツの意味です。
覚えておけばいい情報は、正方形のイメージだけです。
このようにして、情報の減少の原理を働かせています。
またこの方法なら上述②の同じ単語が繰り返し出ていて、同じイメージを使ってしまうという状況を避けれます。
なぜなら、同じ単語が出てきても、他の単語と組み合わせるときに必ず違う組み合わせ方をすることで、違うイメージに見立てられるからです。
これは既知で多様という原理が記憶術ではないと機能しないことがわかっています。
これはすでに知っていることで、多様性に富んだ事柄に変換しないと、すぐに干渉や検索の失敗という現象が起きるという原理です。
これを満たさないのが、円記憶術です。
円記憶術を知りたい方は、ググってみてください。
ここでは説明を割愛させてもらいます。
これで問題は全て解決したかと思うと、ところが、まだ問題があります。
それはコンセプトである脱場所法と想起スピードの高速化がまだまだ満足いく結果になっていないということです。
確かに、パーツを組み合わせ、一つの情報に見立てたことにより、場所はかなり節約できる状況になりました。
しかしそれでもやっぱり場所は、相当量の消費になります。
これを何とかしたい。
また場所に替わる方法がないと、これまたやっぱり想起スピードの高速化は実現しない。
そこで出てくるのが、“名付け”と“圧縮”という方法です。
ここでやっと真打登場というところですね！
名付けとはその名の通り名前を付けることです。
この名付けは動詞でも形容詞でも、もちろん名詞でも何でもいいのでともかく単語に直すことを意味します。
先ほどの正方形だったら、正とついているので、正、つまりrightと名付けます。
rightの意味を含むパーツは、
●●
●
●
無●
（無はスペースと同じ意味です）
です。
このようにして、複数のパーツだったものを一つのパーツに戻します。
そしてそのパーツを使って、組み合わせることでまた一つの見立てたイメージにします。
それが圧縮です。
それではアウトプットの問題である上述③の抽象的イメージが、思い出すときは多義的で思い出しづらいという問題です。
これは連想の形式を模したアウトプットの仕方で解決しました。
どういうことかというと、一つのパーツが意味している単語を一つではなく、一つのパーツが意味している単語が三つあるというものです。
これは理論的には漢字の読みと同じようなことをしています。
つまり漢字も読みが複数個ありますが、あまり混乱することはないということからの思い切った方策です。
これはパーツからの連想が三つあるのと同じです。
しかし、多義的と言っても、その探索範囲は抽象的なイメージを思い出すよりしっかり固定されていて、また狭いものです。
このようにして③の問題を解決しました。
そして最後の上述④の問題ですが、これは全く解決しておりません！
むしろ解決の仕方を教えてほしいくらいです。
そのため今後の課題だと思います。
また他の今後の課題としては、脳の可塑性のどれだけよりよく恩恵を受けれるようにするかも課題です。
ただいま、自己実験していますが、想起スピードの高速化はなされていますが、入力スピードの高速化はあまりなされていない気がします。
新しい単語に対して、どう記憶するかということを思案する時間があるからなのですが、その内この思案時間はなくなるのかが謎でしょうがありません。
追記
対文章式記憶術では全ての情報をパーツ化することにより、“一斉に想起”できるようにするため色々普通の記憶術にはない仕組みを働かせています。
しかし今日では一斉想起できることはデメリットとして“一斉に忘却”するという特性も出てきてしまうことがわかりました。
そこで以下の方法で一斉忘却を防ぐことにしています。
完全に効果を実証したものではありませんが、経験的に上手く一斉忘却を防ぐことができると思われる方法です。
①各パーツに任意で具体的なイメージを当てておく
これは例えば●●●だったら蛇という具体的なイメージを当てはめておくということです。
その具体的イメージを当てはめたパーツで、レゴブロックのように組み合わせて、任意のイメージを作り、見立てることを目指します。
②各パーツを離して配置する
これは
●●●と●だったら例えば
●●●無無●
というように無（スペースの代わり）を間に置いて、パーツ同士を離して何かに見立てるということが大事ということです。
③各パーツを抜いたイメージをしておく
これはどうやら一部のイメージが忘却で抜けても、事前にその抜けたイメージをしておかないと、抜けたイメージがされず、一斉忘却をするようだという点からの対策です。
以上追記でした。
